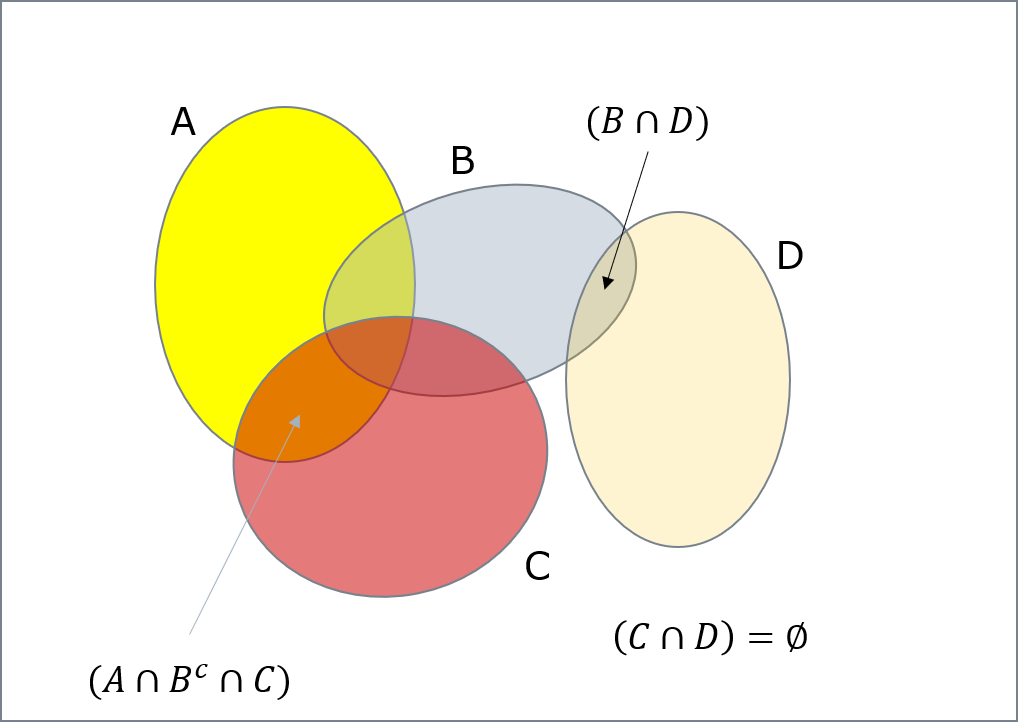
Events are represented as sets, and this by Venn diagrams. It is interesting to remember some properties.
Union \(A\cup B\): when \(A\) or \(B\) or both are observed. In the example: $$(A \cup B) = (A \cap \bar B) \cup (A \cap B) \cup (\bar A \cap B)$$
Intersection\(A\cap B\): when \(A\) and \(B\) are simultaneously observed.
Morgan's laws: $$(A \cup B)^c = (A^c \cap B^c)$$ $$(A \cap B)^c = (A^c \cup B^c)$$
Inclusion An event \(A\) is included in \(B\) when all observations of \(A\) are also observations of \(B\). $$A \subset B$$ Accordingly, $$(A \cap B) \subset (A \cup B)$$
The probability of observing an event \(A\) is noted as \(P(A)\).
$$0 \leq P(A) \leq 1$$
If \(A \subset B\), then $$P(A) \leq P(B)$$
The probabilty of observing \(A\) or \(B\) is: $$P(A \cup B)=P(A)+P(B)-P(A \cap B)$$
If \((A\cap B)=\emptyset \), then \(P(A \cap B)=0\), thus: $$P(A \cup B)=P(A)+P(B)$$
The probability of the complementary of \(A\) is: $$P(\bar A)=1-P(A)$$
The probability of \(A\) given that \(B\) is present is defined as: $$P(A|B)=\frac{P(A \cap B)}{P(B)}$$ In general \(P(A|B) \neq P(A)\). From its definition, it follows that: $$P(A \cap B) = P(A|B) P(B) = P(B|A) P(A)$$ Thus: $$P(A|B)=P(B|A)\frac{P(A)}{P(B)}$$
If \(P(A|B)=P(A)\), then the two events are independent, as there is the same expectative for \(A\) indepndently of the presence of B. In that case: $$P(A \cap B)=P(A)P(B)$$
Interpretation
The probability of a heart stroke is not the same for males and females.The probability of obesity is different for people taking different diets.
The probability of recovering from a health problem depends on age and genetic characteristics.
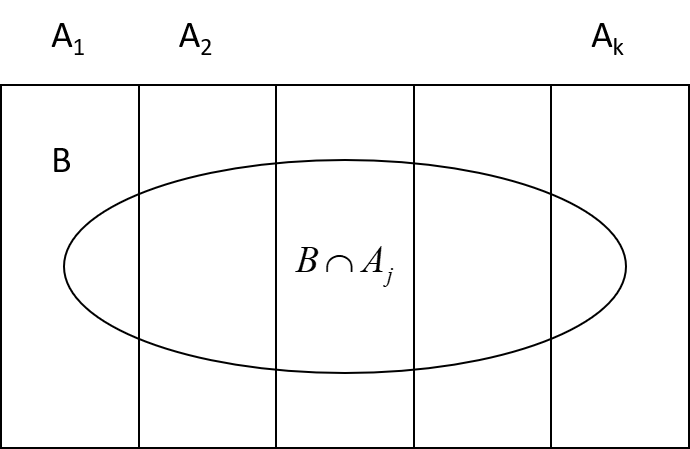
If we have a partition \(A_1,A_2,...,A_k\), and an event \(B\), then we can write: $$B=(A_1\cap B)\cup (A_2 \cap B) \cup ... \cup (A_k \cap B)$$ Then the \(P(B)\) can be written as: $$P(B)=P(A_1\cap B)+ P(A_2 \cap B) + ... +P(A_k \cap B)$$ and finally: $$P(B)=P(B|A_1) P(A_1)+ P(B|A_2) P(A_2) + ... +P(B|A_k) P(A_k)$$
The Baye's theorem describes the probability of an event, based on prior knowledge of conditions that might be related to the event. $$P(A|B)=\frac{P(A \cap B)}{P(B)}=\frac{P(B|A) \times P(A)}{P(B)}=\frac{P(B|A) \times P(A)}{P(B|A) \times P(A)+P(B|\bar A) \times P(\bar A)}$$
Interpretation
For example, the probability of having a disease \((D)\) if the result of a laboratory test is positive (+) can be computed as: $$P(D|+)=\frac{P(+|D)\times P(D)}{P(+|D)\times P(D)+P(+|H)\times P(H)}$$ We can compute this probability if we know the probability that a person that has the disease will give a positive result, i.e. \(P(+|D)\), the probability of a positive result for healthy people, i.e. \(P(+|H)\), and the prevalence of the disease \(P(D)\)Which is the probability of a disease \(D\) given a symptom \(S\)?
We will use the Baye's theorem: $$P(D|S)=\frac{P(D\cap S)}{P(S)}=\frac{P(S|D)\times P(D)}{P(S|D)\times P(D)+P(S|\bar D)\times P(\bar D)}$$ Thus we need to indicate the probability of observing the symptom if the person has the disease: \(P(S|D)\), and this probability for the healthy people: \(P(S|\bar D)\). The probability of having the disease given the symptom depends also on the prevalence of the disease in the population \(P(D)\). The application computes \(P(D|S)\) for the selected probabilities and also the curve showing how this probability changes with the prevalence.
A priori P(D)
A posteriori P(D|S)
Diagnostic test: interpretation
Values of the test performance as indicated by the laboratory
Prevalence of the disease (D) in the population
Proportions in the sample: We simulate a sample of the population according to the indicated size and prevalence of the disease.
Test's results On the obtained sample, we simulate the results of the test according to the sensitivity and especificity selected.
False positive and false negartive rates On the previous table of the results of the test, the proportion with respect the sample size indicates the performance of the test as TNR and FNR (row of healthy) and FPR and TNR (row of disease).
Estimated sensitivity and especificity From the table of result of the test, the column proportions allow estimating the sensitivity and especificity of the test. The obtained values should be close to the indicated by the laboratory if the size of the sample is large. For small samples, these results may be far from the expected.
The simplest diagnostic test produce two possible outcomes: (+) and (-). The positive (+) result is associated with a diagnostic of presence of a disease condition, while a negative (-) result is associated with a healthy diagnostic.
Sensitivity: \(P(+|D)\) Is the probability of obtaining a positive result in the test on an individual that has the disease (D).
Especificity: \(P(-|H)\) Is the probability of obtaining a negative result in the test on a healthy (H) individual.
False positive rate (FPR): \(P(+ \cap H)\) When the test is applied to a population where the prevalence of the disease is \(P(D)\), the FPR is the proportion of subjects that will be healthy with a positive result.
False negative rate (FNR): \(P(- \cap D)\) When the test is applied to a population where the prevalence of the disease is \(P(D)\), the FNR is the proportion of subjects that will have the disease with a negative result.
FNR+FPR: Indicates the probability of an erroneous diafnostic when applying the test on that population.
Expected results of applying the test to the population
Proportion of false positives (FPR): \(P(+\cap H)=P(+|H) \times P(H)\)
Proportion of false negatives (FNR): \(P(-\cap D)=P(-|D) \times P(D)\)
Proportion erroneous diagnostics: \(P(-\cap D)+(P(+\cap H)\)
Positive predictive value (PPV): \(PPV:P(D|+)= \frac{P(+|D)P(D)}{P(+|D)P(D)+P(+|H)P(H)}\)
Negative predictive value (NPV): \(NPV:P(H|-)= \frac{P(-|H)P(H)}{P(-|H)P(H)+P(-|D)P(D)}\)
Simulation
Proportions in the sample
Test's results
False positive and false negative rates
Estimated sensitivity and especificity
Which disease is more probable based on symptoms?
Supose you need to decide among four possible diseases \(D_1, D_2, D_3, D_4\), based on a symptom \(S\).
Indicate your a priori probabilities for each disease and the probability of
a symptom under each of the considered disease. The application computes the posterior
probabilities of the diseases.
A priori probabilities
Which are the probabilities that you assignate to each disease (must add up to 1)?
Probability of the symptom under each disease
Which is the probability of the symptom (S) if a person suffers a given disease?
Probability of observing the symptom in a person selected randomly in this situation:
\(P(S)=P(S/D_1)\times P(D_1)+..+P(S/D_k)\times P(D_k)=\)Probabilities a posteriori compared to the a priori information.
\(P(D_i|S)=\frac{P(S/D_i)\times P(D_i)}{P(S)}\)Which is the probability of a disease \((D)\) given that symptom 1 (\(S_1\)) or symptom 2 (\(S_2\)) are present?
\(P(D|S_1\cup S_2)=\frac{P((S_1\cup S_2)|D)\times P(D)}{P(S_1\cup S_2)}=\frac{P(D) \times [P(S_1|D)+P(S_2|D)-P((S_1 \cap S_2)|D)]}{P(S_1)+P(S_2)-P(S_1 \cap S_2)}\)